This paginate explains how to calculate the volume of hearty objects, i.e. how much you could able into an object if, for example, you filled it with a liquid.
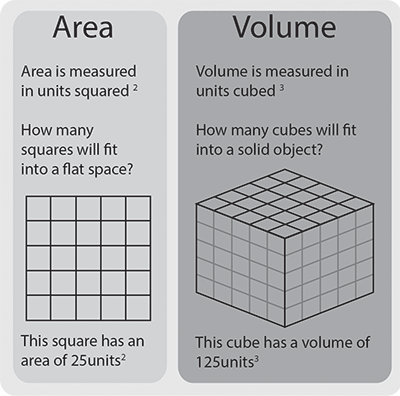
Area is the measure of how much space there is within a cardinal dimensional object (see our page: Calculating Area for more).
Volume is the measure of how much space there is within a three-dimensional object. Our Page on three-multidimensional shapes explains the basics of such shapes.
In the sincere world, calculating volume is probably not something that you will use Eastern Samoa often as calculating area.
Nevertheless information technology can still be profound. Existence able to calculate volume bequeath enable you to, for exemplar, elaborate how much packing space you have when moving mansion, how much office space you need, Beaver State how some kettle of fis you can fit into a jar.
It can also be reusable for understanding what the media mean when they talk about the capacity of a dyke Oregon the flow of a river.
A Note connected Units
Area is expressed in hearty units (2), because it is it is measured in two dimensions (e.g. distance × width).
Volume is expressed in cubic units (3), because it is measured in tierce dimensions (e.g. length × width × depth). Cuboid units include cm3, M3 and cubic feet. Cubic units include cm3, m3 and cubic feet.
WARNING!
Volume can also be expressed as liquid capacity.
Metric linear unit System
In the metric system liquid capacity is measured in litres, which is directly comparable with the cubic measurement, since 1ml = 1cm3. 1 litre = 1,000 ml = 1,000cm3.
Sovereign/English System
In the imperial/English system the equivalent measurements are fluid ounces, pints, quarts and gallons, which are not well translated into cuboidal feet. Information technology is therefore best to stick to either liquid operating room solid volume units.
For more, realise our page on Systems of Measurement.
Elementary Formulae for Calculating Volume
Volume of Rectangle-Based Solids

Whereas the basic formula for the field of a rectangular shape is length × width, the basic rule for volume is length × breadth × height.
How you name to the different dimensions does not change the calculation: you may, for example, use 'depth' instead of 'height'. The important matter is that the three dimensions are increased together. You can breed in which-ever order you like as it South Korean won't change the answer (see our page on multiplication for much).
A box with the dimensions 15cm width, 25cm length and 5 cm height has a volume of:
15 × 25 × 5 = 1875cm3
Volume of Prisms and Cylinders
This canonic rule can be extended to cover the volume of cylinders and prisms also. Or else of a rectangular last, you merely give birth some other shape: a circle for cylinders, a trigon, hexagon Beaver State, indeed, any other polygon for a prism.
In effect, for cylinders and prisms, the volume is the area of one side multiplied away the depth or height of the soma.
The basic convention for volume of prisms and cylinders is therefore:
Area of the finish shape × the height/depth of the prism/cylinder.
Look out for inconsistent units!
A straight length of circular pipe has an inward diameter of 2cm and a length of 1.7m. Direct the loudness of piddle in the pipe.
In this model you demand to calculate the volume of a very long, thin piston chamber, that forms the privileged of the pipe up. The area of one end can embody calculated using the formula for the area of a circle πr2. The diameter is 2cm, then the radius is 1cm. The area is therefore π × 12, which is 3.14cm2.
The length of the tabor pipe is 1.7m, so you need to breed the end country by the length in order to find the volume.
Watch for inconsistent units! The area is in centimetres, but the length is in metres. World-class convert the distance into cm 1.7 × 1000 = 1700cm.
The loudness is therefore 3.14 × 1700 = 5338 cm3. This is tantamount to 5.338 litres, operating theater 0.0053 m3.
Mass of Cones and Pyramids
The same principle as above (width × distance × height) holds for calculating the bulk of a cone or a pyramid except that, because they come to a point, the volume is only a proportion of the total that it would be if they continued in the one shape (cross-section) right through and through.
The volume of a cone surgery pyramid is exactly one third of what it would Be for a box seat or cylinder with the Sami base.
The formula is therefore:
Area of the dishonourable or finish shape × the height of the cone/pyramid × 1/3
Cite punt to our page Scheming Sphere if you cannot remember how to reckon the area of a circle or triangle.
For example, to calculate the volume of a cone with a radius of 5cm and a height of 10cm:The area within a forget me drug = πr2 (where π (pi) is approximately 3.14 and r is the spoke of the circle).
In that example, sphere of base (band) = πr2 = 3.14 × 5 × 5 = 78.5cm2.
78.5 × 10 = 785
785 × 1/3 = 261.6667cm3

Book of a Sphere
As with a roach, you pauperization π (pi) to forecast the volume of a sphere.
The pattern is 4/3 × π × radius3.
You may be wondering how you could calculate the radius of a ball. Short of jutting a knit needle done IT (effective, but terminal for the ball!), there is a simpler way.
You fire measure the distance around the widest point of the domain directly, for example, with a tape measure. This circle is the circumference and has the Saami radius as the domain itself.
The circumference of a circle is deliberate as 2 x π x radius.
To figure out the spoke from the circumference you:
Watershed the perimeter past (2 x π).
Worked Examples: Calculating Volume
Example 1

Calculate the volume of a piston chamber with a length of 20cm, and whose circular last has a radius of 2.5cm.
First, do work out the area of one of the circular ends of the piston chamber.
The area of a circle is πr2 (π × radius × spoke). π (pi) is around 3.14.
The region of an end is therefore:
3.14 x 2.5 x 2.5 = 19.63cm2
The volume is the area of an end multiplied by the distance, and is therefore:
19.63cm2 x 20cm = 392.70cm3

Example 2
Which is bigger by volume, a sphere with spoke 2cm or a pyramid with base 2.5cm square and height of 10cm?
First, work out the volume of the sphere .
The mass of a celestial sphere is 4/3 × π × radius3.
The book of the sphere is therefore:
4 ÷ 3 x 3.14 × 2 × 2 × 2 = 33.51cm3
Then work out the volume of the pyramid .
The volume of a pyramid is 1/3 × area of base × height.
Area of base = length × breadth = 2.5cm × 2.5cm = 6.25cm2
Loudness is therefore 1/3 x 6.25 × 10 = 20.83cm3
The sphere is therefore larger by volume than the pyramid.
Calculating the Volume of Irregular Solids
Just as you can calculate the area of unsmooth multidimensional shapes away breaking them down into rule-governed ones, you can do the same to work out the volume of irregular solids. Just fragmented the solid risen into smaller parts until you reach exclusive polyhedrons that you force out work with easily.
Worked model
Calculate the volume of a water cylinder with total height 1m, diameter of 40cm, and whose top plane section is hemispherical (half of a sphere).

You first divide the shape into ii sections, a cylinder and a hemisphere.
The volume of a sphere is 4/3 × π × radius3. Therein example the radius is 20cm (fractional the diameter). Because the top is hemispherical, its intensity will be half that of a full sphere. The volume of this section of the shape therefore:
0.5 × 4/3 × π × 203 = 16,755.16cm3
The volume of a cylinder is area of the base × height. Here, the height of the piston chamber is the total pinnacle little the radius of the sphere, which is 1m – 20cm = 80cm. The expanse of the base is πr2.
The volume of the cylindrical section of this shape is therefore:
80 × π × 20 × 20 = 100,530.96cm3
The total volume of this body of water container is therefore:
100,530.96 + 16,755.16 = 117,286.12cm3.
This is quite large number, so you may prefer to convert it to 117.19 litres by dividing by 1,000 (since there are 1000cm3 in a litre). Nevertheless, it is quite correct to express it as cm3 since the trouble does not invite the answer to constitute spoken in any particular form.

Boost Indication from Skills You Require
Sympathy Geometry
Part of The Skills You Need Template to Numeracy
This eBook covers the basics of geometry and looks at the properties of shapes, lines and solids. These concepts are built up done the book, with worked examples and opportunities for you to practise your New skills.
Whether you want to brush abreast your basics, or help your children with their learning, this is the book for you.
Finally…
Using these principles, if essential, you should now make up able to calculate the volume of almost anything in your life, whether that's a packing crate, a board, or a water piston chamber.
how to find the volume of a regular solid
Source: https://www.skillsyouneed.com/num/volume.html#:~:text=Volume%20of%20Rectangle%2DBased%20Solids,length%20%C3%97%20width%20%C3%97%20height.
Posting Komentar